|
|
|
|
Коши Огюстен Луи
(Cauchy Augus-tin Louis) (21.8.1789,
Париж,-23.5. 1857, Co.) - французский математик, иностранный
почётный чл. Петербургской АН (1831), чл. Парижской
АН (1816). Окончил Политехнич. школу (1807) и Школу
мостов и дорог (1810) в Париже. В 1810-13 работал инженером
в Шербуре. В 1816-30 преподавал в Политехнич. школе
и в Коллеж де Франс, с 1848 - в Парижском ун-те и в
Коллеж де Франс. Труды К. относятся к различным об-лйе-гям
математики (преимущественно к математич. анализу) и
математич. физики.
http://matan.alpol.ru
|
|
НЕРАВЕНСТВО КОШИ
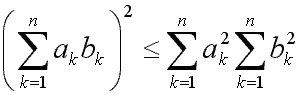
имеющее место для конечных
сумм; очень важное и наиболее употребительное в различных
областях математики и математической физики неравенство.
http://vadim-soft.narod.ru
|
 |
КАРДАНО Джероламо
(Иеронимус) (Cardano Girolamo)
(24.9.1501, Па-вия,- 21.9.1576, Рим) - итальянский математик,
философ и врач. С именем К. связывают формулу решения
в радикалах неполного кубич. уравнения (формулу Кардано).
Работы К. сыграли большую роль в развитии алгебры. Одним
из первых в Европе он стал допускать отрицательные и
мнимые корни уравнений. Занимался вопросами передачи
движения, теорией рычагов (карданная передача, карданов
подвес). Развивал своеобразную натурфилософию под влиянием
Николая Кузанского.
http://matan.alpol.ru/persons/10/14.htm
|
КАРДАНО ФОМУЛА
Формула, выражающая корни кубического
уравнения: x3+px+q=0 (*) через его коэффициенты.
К виду (*) приводится всякое кубическое уравнение.
Ф.К. записывается так:
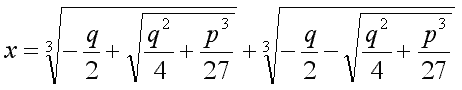
Выбирая произвольно значение
первого кубического радикала, следует выбрать то значение
второго радикала (из трёх возможных), которое в произведении
с выбранным значением первого радикала даёт (-p/3).
Таким образом получают все три корня уравнения (*).
До сих пор не ясно, кому принадлежит Ф.К.: Дж. Кардано,
Н. Тарталье или С. Ферро. Ф.К. относится к XVI в.
http://vadim-soft.narod.ru
|
 |
КАССИНИ Джованни Доменико
(Жан Доминик) (Cassini Giovanni
Domenico) (8.6.1625, Перинальдо,- 14.9.1712, Париж)
- французский астроном, чл. Парижской АН (1669). Открыл
вращение Юпитера (1665) и Марса (1666), деление кольца
Сатурна на внутреннее и внешнее. Его именем названа
плоская алгебраич. кривая 4-го порядка (овал Кассини),
к-рую К. рассматривал при попытках определить орбиту
Земли.
http://matan.alpol.ru
|
КАССИНИ ОВАЛЫ,
алгебраические кривые 4-го порядка. Множество точек,
произведение расстояний которых от двух данных точек
F1 и F2 постоянно.
Энциклопедия Кирилла и Мефодия,
2003
|
 |
ЛОБАЧЕВСКИЙ Николай Иванович
[20.11(1.12). 1792, Нижний Новгород, ныне г. Горький,-
12 (24). 2.1856, Казань] - русский математик, создатель
неевклидовой геометрии, мыслитель-материалист. Родился
в семье бедного чиновника. Почти всю свою жизнь Л.
провёл в Казани. Там он учился в гимназии (1802-07),
затем в Казанском ун-те (1807-11). По окончании университета
был оставлен при нём; в 1811 утверждён магистром,
в 1814 адъюнктом, в 1816 экстраординарным и в 1822
ординарным проф., был также деканом физико-ма-тематич.ф-та
(1820- 22, 1823-25) и ректором университета (1827-
46). В последний период своей жизни (1846-56) Л.-помощник
попечителя Казанского учебного округа.
http://matan.alpol.ru
|
ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ,
построенная в 1826 Н. И. Лобачевским геометрическая
теория, основанная на тех же основных посылках, что
и обычная евклидова геометрия, за исключением аксиомы
(постулата) о параллельных. Евклидова аксиома гласит:
в плоскости через точку, не лежащую на данной прямой,
можно провести одну, и только одну, прямую, параллельную
данной, т. е. ее не пересекающую. В геометрии Лобачевского
эта аксиома заменена следующей: в плоскости через
точку, не лежащую на данной прямой, можно провести
более одной прямой, не пересекающей данной. В геометрии
Лобачевского многие теоремы отличны от аналогичных
теорем евклидовой геометрии; напр., сумма углов треугольника
меньше двух прямых, два подобных треугольника всегда
равны между собой. Несмотря на внешнюю парадоксальность
этих выводов, геометрия Лобачевского оказалась логически
совершенно равноправной с евклидовой. Открытие неевклидовой
геометрии Лобачевского внесло коренные изменения в
представления о природе пространства.
Энциклопедия Кирилла и Мефодия,
2003
|
 |
ЛАГРАНЖ Жозеф Луи
(Lagrange Joseph Louis) (25.1.1736, Турин,- 10.4.1813,
Париж) -французский математик и механик, иностранный
почётный чл. Петербургской АН (1776), чл. Парижской
АН (1772). Родился в семье обедневшего чиновника.
Самостоятельно изучал математику. В 19 лет стал проф.
в артиллерийской школе Турина. В 1759 избран чл. Берлинской
АН, а в 1766-87 - директором её Математич. класса.
В 1787 переехал в Париж; с 1795 проф. Нормальной школы,
с 1797 - Политехнич. школы.
http://matan.alpol.ru
|
ФОРМУЛА ЛАГРАНЖА,
одна из основных формул дифференциального исчисления,
дающая связь между приращением функции f(x)
и значениями её производной, эта формула имеет вид:
f(b)-f(a)=(b-a)f'(c),
где с
- некоторое число, удовлетворяющее неравенствам a<с<b.
http://www.rubricon.com
|
| |
МЕНЕЛАЙ Александрийский
(MeveXaog) (1 в.) -древнегреческий
математик и астроном. Автор работ по сферич. тригонометрии:
6 книг о вычислении хорд и 3 книги "Сферики"
(сохранились в арабском переводе). Для получения формул
сферич. тригонометрии использовал теорему о прямой,
пересекающей стороны треугольника (теорема Менелая).
http://matan.alpol.ru
|
ТЕОРЕМА МЕНЕЛАЯ
Если прямая пересекает стороны треугольника
АВС или их продолжения в точках C', A' и B' , то справедливо
соотношение:
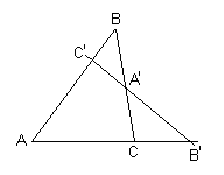
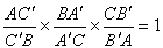 (*)
(*)
Отношение отрезков
берётся положительным, если прямая пересекает сторону
треугольника, и отрицательным, если прямая пересекает
продолжение стороны. Справедливо и обратное выражение:
если выполняется равенство (*), где
A, B, C
- вершины треугольника, а A', B',
C' лежат на одной прямой. Теорему Менелая
можно сформулировать в виде критерия расположения
трёх точек A', B' и C'
на одной прямой: для того, чтобы 3 точки A',
B' и C' лежали на одной
прямой, необходимо и достаточно, чтобы выполнялось
соотношение (*), где A,
B, C - вершины треугольника,
а A', B', C'
принадлежат соответственно прямым BC,
AC и AB.
http://vadim-soft.narod.ru
|
| |
МОЛЬВЕЙДЕ Карл Брандау
(Mollweide Karl Brandau) (3.2.1774,
Воль-фенбюттель,-10.3.1825, Лейпциг) - немецкий математик
и астроном. Известны (1808) формулы Мольве и д е для
решения косоугольных треугольников.
http://matan.alpol.ru
|
ФОРМУЛЫ МОЛЬВЕЙДЕ
Формулы плоской
тригонометрии, выражающие следующую зависимость между
сторонами (их длинами) и углами треугольника:
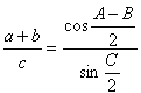 ; ;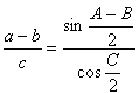 ,
,
где a, b, c -
стороны, а A, B, C - углы треугольника. Ф.М. названы
по имени немецкого математика К. Мольвейде, использовавшего
их, хотя эти формулы были известны и другим математикам.
http://vadim-soft.narod.ru
|
 |
МИНКОВСКИЙ Герман
(Minkowski Hermann) (22.6.1864, Алексоты Минской губ.,
-12.1.1909, Гёттинген) - немецкий математик и физик,
проф. ун-тов в Бонне (с 1893), Кенигсберге (с 1894),
Цюрихе (с 1896), Гёттингене (с 1902). Разработал т.
н. геометрию чисел, в которой употребляются геомет-рич.
методы решения вопросов теории чисел. От геометрии
чисел М. перешёл к работам по теории многогранников
и геометрии выпуклых тел (теоремы Минковского, 1896),
где им были получены важные общие результаты (напр.,
неравенство Минковского, 1896). М.- автор работ по
математич. физике, гидродинамике и теории капиллярности,
в 1907-08 дал геометрич. интерпретацию кинематики
специальной теории относительности, введя т. н. пространство
Минковского.
http://matan.alpol.ru
|
НЕРАВЕНСТВО МИНКОВСКОГО.
Неравенство для p-х степеней чисел, имеющее вид:
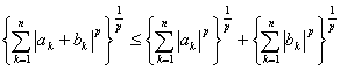 , ,
где целое p>1,
а ak и bk
- неотрицательные числа. Неравенство Минковского является
обобщением известного "неравенства треугольника",
утверждающего, что длина одной стороны треугольника
не больше суммы длин двух других его сторон; для n-мерного
пространства расстояние между точками x=(x1,
x2, …, xn) и y=(y1, y2, …, yn)
определяется числом
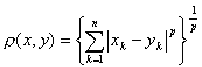
http://vadim-soft.narod.ru
|
|
|