|
|
|
|
ФАЛЕС Милетский (ок.
625-547 до н. э.) - древнегреческий математик, астроном
и философ. Основатель ионийской (милетской) школы натурфилософии.
Предполагают, что Ф. был первым греческим геометром.
Ему приписывают доказательства нескольких геометрич.
теорем (напр., теорема Фалеса об отрезках, лежащих на
двух прямых, рассекаемых параллельными прямыми).
http://matan.alpol.ru
|
|
ТЕОРЕМА ФАЛЕСА
Одна из теорем элементарной
геометрии о пропорциональных отрезках. Теорема утверждает,
что если на одной из сторон угла от его вершины последовательно
отложить равные между собой отрезки и через концы этих
отрезков провести параллельные прямые, пересекающие
вторую сторону угла, то на второй стороне угла отложатся
также равные между собой отрезки. Частный случай теоремы
выражает некоторые свойства средней линии треугольника.
http://vadim-soft.narod.ru
|
|
|
ФЕРМА Пьер (Fermat
Pierre) (17.8. 1601, Бомон-де-Ломань,- 12.1.1665, Кастр)
- французский математик. По профессии юрист, с 1631
был советником парламента в Тулузе. Автор ряда выдающихся
работ, большинство из к-рых было издано после смерти
Ф. его сыном под назв. "Разные математические сочинения"
("Varia opera mathematica", Tolosae, 1679);
при жизни Ф. полученные им результаты становились известны
учёным благодаря переписке и личному общению. Ф. является
одним из создателей теории чисел, где с его именем связаны
две знаменитые теоремы: в е-ликая теорема Ферма и малая
теорема Ферма.
http://matan.alpol.ru
|
|
ВЕЛИКАЯ ТЕОРЕМА ФЕРМА.
Уравнение xn + yn
= zn (где n - целое число большее двух) не
имеет решений в целых положительных числах. Несмотря
на утверждение П. Ферма о том, что ему удалось найти
удивительное доказательство В.Ф.Т., которое он не приводит
из-за недостатка места (это замечание написано было
П. Ферма на полях книги Диофанта), до недавнего времени
(середина 90-х) В.Т.Ф. в общем виде доказана не была.
http://vadim-soft.narod.ru
|
| |
ХОРЕЗМИ, аль-Хорезми Абу Абдалла
Мухаммед бен Муса аль-Маджуси (787,
Хива,- ок. 850) - среднеазиатский математик и астроном.
Автор арифметич. трактата, который в 12 в. был переведён
с арабского на латинский язык и по которому в Европе
познакомились с индийской позиционной системой счисления.
В алгебраич. труде X. ["Краткая книга восполнения
и противопоставления" (Китаб мухтасар аль-джебр
вал-мукабала)] алгебра впервые рассматривается как самостоятельная
отрасль математики, вводятся правила действий с алгебраич.
количествами и систематически решаются уравнения 1гй
и 2-й степеней. Этот трактат долгое время служил основным
руководством по алгебре в странах Европы.
http://matan.alpol.ru
|
|
АЛГОРИТМ.
Название операции "аль-джебр", состоящей в
перенесении членов из одной стороны уравнения в другую
с изменением знака, впоследствии стало названием раздела
математики (алгебра). Имя аль-Хорезми (латинизированное
Algorithmi) вошло в математику вначале как обозначение
арифметики с помощью индийских чисел, а затем как общее
название (алгоритм) всякой системы вычислений, выполняемых
по строго определённым правилам.
http://matan.alpol.ru
|
| |
ЦЕРМЕЛО Эрнст
(Zermelo Ernst) (27.7. 1871, Берлин,-21.5.1953,
Фрайбург) - немецкий математик. В 1894 окончил Берлинский
ун-т, с 1926 проф. университета в Фрайбурге. Основные
труды по теории множеств, в которой он ввёл общую аксиоматику
(включающую известную аксиому Цермело, или аксиому свободного
выбора) и с помощью названной аксиомы доказал, что всякое
множество может быть вполне упорядочено (теорема Цермело).
Аксиома свободного выбора играет существенную роль не
только в теории множеств, но и во всём классич. анализе,
и вопрос о её допустимости вызывал и вызывает оживлённые
споры, стимулирующие развитие оснований математики и математич.
логики. Занимался также вариационным исчислением и вопросами
приложения теории вероятностей к статистич. физике.
http://matan.alpol.ru
|
|
ТЕОРЕМА ЦЕРМЕЛО:
всякое множество может быть упорядоченно
http://matan.alpol.ru
|
|
|
ЧЕВА Джованни (Ceva
Giovanni) (3.3. 1648, Милан,- 13.12.1734, Мантуя) -
итальянский инженер и математик. Окончил Пизанский ун-т.
Основные работы по геометрии и механике. Доказал (1678)
теорему о соотношении отрезков нек-рых прямых, пересекающих
треугольник (теорема Чевы). Построил учение о секущих,
которое положило начало синтетич. геометрии; оно изложено
в соч. "О взаимно пересекающихся прямых" ("De
line is rectis se inuicem secantibus", Mediolani,
1678).
http://matan.alpol.ru
|
|
ТЕОРЕМА ЧЕВЫ. Если
прямые, соединяющие вершины треугольника АВС с
точкой О, лежащей в плоскости треугольника,
пересекают противоположные стороны (или их продолжения)
соответственно в точках A' B' C', то справедливо
равенство:
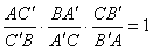 (*) (*)

При этом отношение отрезков
рассматривается как положительное, если эти отрезки
имеют одинаковое направление, и отрицательное - в противном
случае.
Т.Ч. можно записать и в такой форме: (ABC')*(BCA')*(CAB')
= 1, где (АВС') - простое отношение
трёх точек A, B и C'.
Справедлива и обратная теорема: если точки C',
A', B' расположены соответственно
на сторонах AB, BC и
СА треугольника или их продолжениях так, что
выполняется равенство (*), то прямые АА',
BB' и CC', пересекаются
в одной точке или параллельны (пересекаются в несобственной
точке).
Прямые AA', BB' и СС',
пересекающиеся в одной точке и проходящие через вершины
треугольника, называются прямыми Чевы или чевианами.
http://vadim-soft.narod.ru
|
|
|